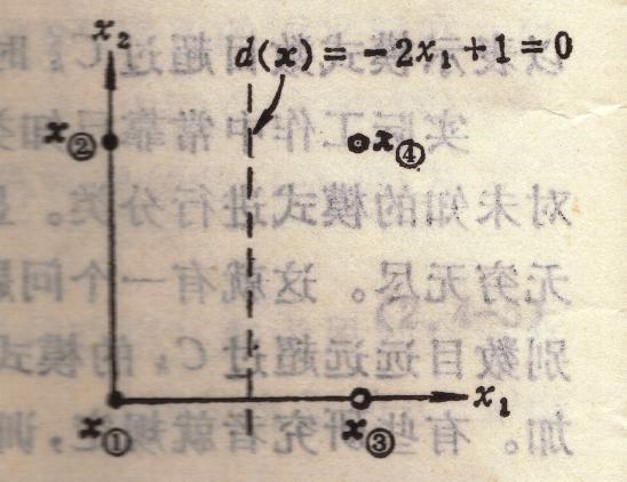
作业如下

代码如下
# -*- coding: utf-8 -*-
"""感知器算法.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1uMcSUjFe0Sz3yInk2ir5xoBnFwmlsIpp
"""
# -*- coding:utf-8
import numpy as np
a = [[0,0,0],[1,0,0],[1,0,1],[1,1,0]]
b = [[0,0,1],[0,1,1],[0,1,0],[1,1,1]]
dim=3
#数据定义
a_num = len(a)
b_num = len(b)
a_array=[]
for i in range(a_num):
a[i].append(1)
tmp_narry = np.array(a[i])
print(tmp_narr)
a_array.append(tmp_narry)
# 对属于b的样本,先增广,再乘以-1
b_array=[]
for i in range(b_num):
b[i].append(1)
b[i] = np.dot(b[i],-1)
tmp_narry = np.array(b[i])
print(tmp_narr)
b_array.append(tmp_narry)
array = a_array+b_array
# 设定初始的w为(0,0,0,0)T
w = np.zeros(dim+1).T
# 取矫正向量为1
C = 1
# 分别为参数的序号和迭代的次数
w_num = 0
iter_num = 1
while True:
#flag默认为false,如果本轮迭代中出现了分类错误的情况
#则变更为True
flag = False
print("第%d轮迭代:"%iter_num)
for arr in array:
res = np.dot(arr,w)
print(arr,"*",w,end='')
if res<=0:
print("="+str(res)+"<=0",end=' ')
print("故w("+str(w_num+1)+")=w("+str(w_num)+")+",arr)
w = w + np.dot(arr,C)
flag=True
else:
print("="+str(res)+">0",end=' ')
print("故w("+str(w_num+1)+")=w("+str(w_num)+")")
w_num = w_num + 1
iter_num = iter_num + 1
#迭代次数超过999次先结束运行
if flag==False or iter_num>999:
break
print("w:",w)
print("d(x)="+str(w[0])+"*X1+"+str(w[1])+"*X2+"+str(w[2])+"*X3+"+str(w[3]))
点此下载ipynb文件(可以直接在jupyter或colab中运行)
运行结果为:
第1轮迭代:
[0 0 0 1] * [0. 0. 0. 0.]=0.0<=0 故w(1)=w(0)+ [0 0 0 1]
[1 0 0 1] * [0. 0. 0. 0.5]=0.5>0 故w(2)=w(1)
[1 0 1 1] * [0. 0. 0. 0.5]=0.5>0 故w(3)=w(2)
[1 1 0 1] * [0. 0. 0. 0.5]=0.5>0 故w(4)=w(3)
[ 0 0 -1 -1] * [0. 0. 0. 0.5]=-0.5<=0 故w(5)=w(4)+ [ 0 0 -1 -1]
[ 0 -1 -1 -1] * [ 0. 0. -0.5 0. ]=0.5>0 故w(6)=w(5)
[ 0 -1 0 -1] * [ 0. 0. -0.5 0. ]=0.0<=0 故w(7)=w(6)+ [ 0 -1 0 -1]
[-1 -1 -1 -1] * [ 0. -0.5 -0.5 -0.5]=1.5>0 故w(8)=w(7)
第2轮迭代:
[0 0 0 1] * [ 0. -0.5 -0.5 -0.5]=-0.5<=0 故w(9)=w(8)+ [0 0 0 1]
[1 0 0 1] * [ 0. -0.5 -0.5 0. ]=0.0<=0 故w(10)=w(9)+ [1 0 0 1]
[1 0 1 1] * [ 0.5 -0.5 -0.5 0.5]=0.5>0 故w(11)=w(10)
[1 1 0 1] * [ 0.5 -0.5 -0.5 0.5]=0.5>0 故w(12)=w(11)
[ 0 0 -1 -1] * [ 0.5 -0.5 -0.5 0.5]=0.0<=0 故w(13)=w(12)+ [ 0 0 -1 -1]
[ 0 -1 -1 -1] * [ 0.5 -0.5 -1. 0. ]=1.5>0 故w(14)=w(13)
[ 0 -1 0 -1] * [ 0.5 -0.5 -1. 0. ]=0.5>0 故w(15)=w(14)
[-1 -1 -1 -1] * [ 0.5 -0.5 -1. 0. ]=1.0>0 故w(16)=w(15)
第3轮迭代:
[0 0 0 1] * [ 0.5 -0.5 -1. 0. ]=0.0<=0 故w(17)=w(16)+ [0 0 0 1]
[1 0 0 1] * [ 0.5 -0.5 -1. 0.5]=1.0>0 故w(18)=w(17)
[1 0 1 1] * [ 0.5 -0.5 -1. 0.5]=0.0<=0 故w(19)=w(18)+ [1 0 1 1]
[1 1 0 1] * [ 1. -0.5 -0.5 1. ]=1.5>0 故w(20)=w(19)
[ 0 0 -1 -1] * [ 1. -0.5 -0.5 1. ]=-0.5<=0 故w(21)=w(20)+ [ 0 0 -1 -1]
[ 0 -1 -1 -1] * [ 1. -0.5 -1. 0.5]=1.0>0 故w(22)=w(21)
[ 0 -1 0 -1] * [ 1. -0.5 -1. 0.5]=0.0<=0 故w(23)=w(22)+ [ 0 -1 0 -1]
[-1 -1 -1 -1] * [ 1. -1. -1. 0.]=1.0>0 故w(24)=w(23)
第4轮迭代:
[0 0 0 1] * [ 1. -1. -1. 0.]=0.0<=0 故w(25)=w(24)+ [0 0 0 1]
[1 0 0 1] * [ 1. -1. -1. 0.5]=1.5>0 故w(26)=w(25)
[1 0 1 1] * [ 1. -1. -1. 0.5]=0.5>0 故w(27)=w(26)
[1 1 0 1] * [ 1. -1. -1. 0.5]=0.5>0 故w(28)=w(27)
[ 0 0 -1 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(29)=w(28)
[ 0 -1 -1 -1] * [ 1. -1. -1. 0.5]=1.5>0 故w(30)=w(29)
[ 0 -1 0 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(31)=w(30)
[-1 -1 -1 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(32)=w(31)
第5轮迭代:
[0 0 0 1] * [ 1. -1. -1. 0.5]=0.5>0 故w(33)=w(32)
[1 0 0 1] * [ 1. -1. -1. 0.5]=1.5>0 故w(34)=w(33)
[1 0 1 1] * [ 1. -1. -1. 0.5]=0.5>0 故w(35)=w(34)
[1 1 0 1] * [ 1. -1. -1. 0.5]=0.5>0 故w(36)=w(35)
[ 0 0 -1 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(37)=w(36)
[ 0 -1 -1 -1] * [ 1. -1. -1. 0.5]=1.5>0 故w(38)=w(37)
[ 0 -1 0 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(39)=w(38)
[-1 -1 -1 -1] * [ 1. -1. -1. 0.5]=0.5>0 故w(40)=w(39)
w: [ 1. -1. -1. 0.5]
d(x)=1.0X1+-1.0X2+-1.0*X3+0.5