方法
使用了下面四个库
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from matplotlib import pyplot as plt
关闭掉科学计数法的显示
np.set_printoptions(suppress=True)
读取数据
数据以csv文件的形式存储（见文章最后），使用numpy的loadtxt方法读取
这个方法要求每一行的数据量必须是一样的，不然会报错
with open("data.csv","r") as f:
data = np.loadtxt(f,delimiter = ",")
特征构造
把1x1的列向量，构造成1xn的列向量(例如5x1)
比如输入5,输出的是一个numpy的ndarray变量[5 25 125 625 3125]
data[0]为数据的第一行。reshape是对矩阵进行变化，-1是不指定具体的数值，由计算机来决定，所以reshape(-1,1)就是把数据变成一列
最后使用fit_transform方法获得新的特征
poly_reg = PolynomialFeatures(degree=5)
x_poly = poly_reg.fit_transform(data[0].reshape(-1,1))
转换后的效果如下图所示
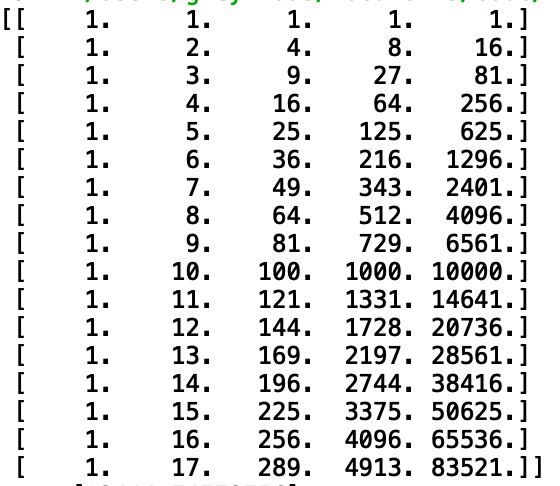
回归分析
接下来把x_poly作为一个多元变量，进行线性回归即可
首先是模型的训练
clf = LinearRegression()
clf.fit(x_poly,data[rown].reshape(-1,1))
训练完成后可以预测结果
day_range=np.linspace(begin_day,begin_day + day_num - 1,day_num)
result = clf.predict(poly_reg.fit_transform(day_range.reshape(-1,1)))
获取线性回归模型的具体参数
clf.coef_ #参数
clf.intercept_ #截距
画图
plt.plot(np.arange(1,len(data[0])+1),data[rown],color='g',linestyle='--',marker='o',label='true')
plt.plot(day_range,result,color=color,linestyle='--',marker='.',label='predict')
plt.title("2019-nCov")
plt.legend()
plt.show()
训练数据
数据来源于卫健委每日发布的数据，记录成csv格式
第一行相当于自变量x，对应着第i天
第二行为武汉市的确诊人数，第三行是全国的确诊人数，第四行是疑似病例
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21
27,41,45,62,121,198,258,363,425,495,572,618,698,1590,1905,2261,2639,3215,4109,5142,6384
27,41,45,62,121,198,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791,14380,17205,20438
0,0,0,0,0,0,54,37,393,1072,1965,2684,5794,6973,9239,12167,15238,17988,19544,21588,23214
预测结果
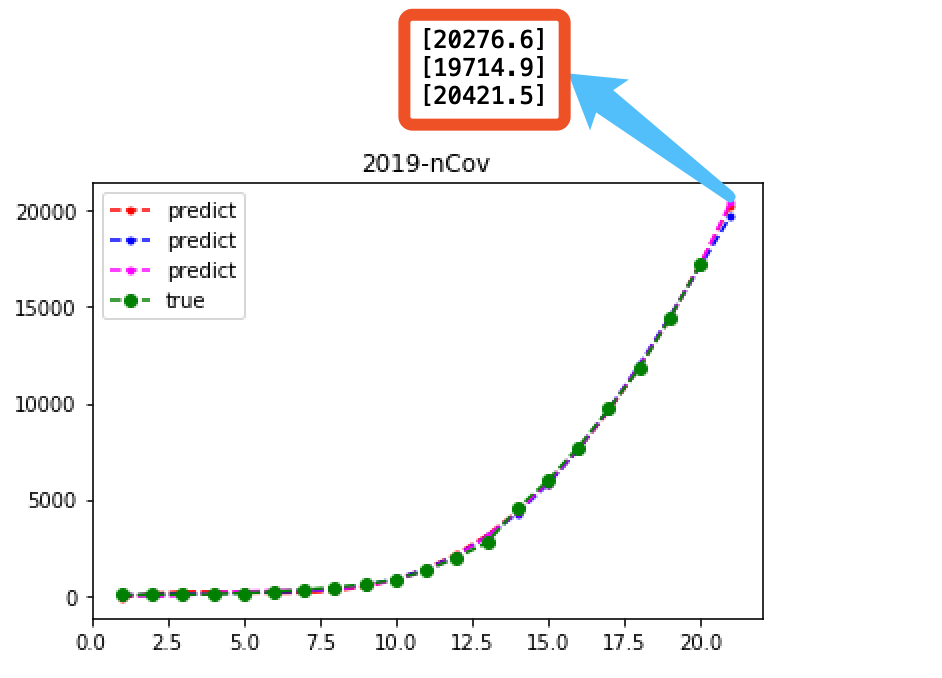实际人数：20438人
| / | 2020/1/29 | 2020/1/30 | 2020/1/31 | 2020/2/1 | 2020/2/2 | 2020/2/3 |
|---|---|---|---|---|---|---|
| 4次回归 | 8448.4 | 10365.7 | 12444.7 | 14578.9 | 17254.8 | 20276.6 |
| 5次回归 | 8305.4 | 9769.4 | 11623 | 13631.5 | 16491.4 | 19714.9 |
| 6次回归 | 7658.5 | 8922.6 | 11065.7 | 13412.3 | 16865.1 | 20421.5 |
| 7次回归 | 6790 | 8537.5 | 11540.7 | 14280.6 | 18131.7 | 21436.5 |
| 真实 | 7711 | 9692 | 11791 | 14380 | 17205 | 20438 |
原始代码
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from matplotlib import pyplot as plt
def predict_new(clf,data,rown,degree,color):
begin_day = 1
day_num = 22
poly_reg = PolynomialFeatures(degree=degree)
x_poly = poly_reg.fit_transform(data[0].reshape(-1,1))
#print(x_poly)
clf.fit(x_poly,data[rown].reshape(-1,1))
day_range=np.linspace(begin_day,begin_day + day_num - 1,day_num) # [1,2,...,day_num]
result = clf.predict(poly_reg.fit_transform(day_range.reshape(-1,1)))
print(" ",np.around(result[-1],decimals=1))
plt.plot(day_range,result,color=color,linestyle='--',marker='.',label='predict')
def predict(clf,data):
rown=2
plt.figure()
predict_new(clf,data,rown,4,'red')
predict_new(clf,data,rown,5,'blue')
predict_new(clf,data,rown,6,'fuchsia')
predict_new(clf,data,rown,7,'orange')
plt.plot(np.arange(1,len(data[0])+1),data[rown],color='g',linestyle='--',marker='o',label='true') # 画出真实值
plt.title("2019-nCov")
plt.legend()
plt.show()
def read_data():
with open("data.csv","r") as f:
data = np.loadtxt(f,delimiter = ",")
data = data[...,:] # 对数据切片，回溯前几天的预测值，对比准确性时用到
print()
return data
if __name__ == "__main__":
print()
np.set_printoptions(suppress=True)
data =read_data()
clf = LinearRegression()
predict(clf,data)