最新日志

• 【Python】matplotlib画图笔记

  2020-01-30

  笔记

  Python
  • 属性
    • 颜色
    • marker属性

  属性

  颜色

  

  marker属性

  用来定义点的形状 符号|解释 –|– .|点标记 ,|pixel marker o|粗点标记 v|朝下的三角箭头 ^|朝上的三角箭头 <|向左的实心箭头 >|向右的实心箭头 1|tri_down marker 2|tri_up marker 3|tri_left marker 4|tri_right marker s|方块 p|五边形

  • *标识
    h	hexagon1 marker
    H	hexagon2 marker

  • +标识
    x	x的标识
    D	diamond marker
    d	thin_diamond marker
    |	竖线标识
    _	横线标识

  Read All

  ---

• 【机器学习】使用sklearn对武汉新型冠状病毒人数进行回归分析

  2020-01-28

  学习

  sklearn
  • 方法
    • 读取数据
    • 特征构造
    • 回归分析
    • 画图
    • 训练数据
  • 预测结果
  • 原始代码
    • 参考

  方法

  使用了下面四个库

  import numpy as np
  from sklearn.preprocessing import PolynomialFeatures
  from sklearn.linear_model import LinearRegression
  from matplotlib import pyplot as plt
  

  关闭掉科学计数法的显示

  np.set_printoptions(suppress=True)
  

  读取数据

  数据以csv文件的形式存储（见文章最后），使用numpy的loadtxt方法读取
  这个方法要求每一行的数据量必须是一样的，不然会报错

  with open("data.csv","r") as f:
      data = np.loadtxt(f,delimiter = ",")
  

  特征构造

  把1x1的列向量，构造成1xn的列向量(例如5x1)
  比如输入5,输出的是一个numpy的ndarray变量[5 25 125 625 3125]
  data[0]为数据的第一行。reshape是对矩阵进行变化，-1是不指定具体的数值，由计算机来决定，所以reshape(-1,1)就是把数据变成一列
  最后使用fit_transform方法获得新的特征

  poly_reg = PolynomialFeatures(degree=5)
  x_poly = poly_reg.fit_transform(data[0].reshape(-1,1))
  

  转换后的效果如下图所示
  

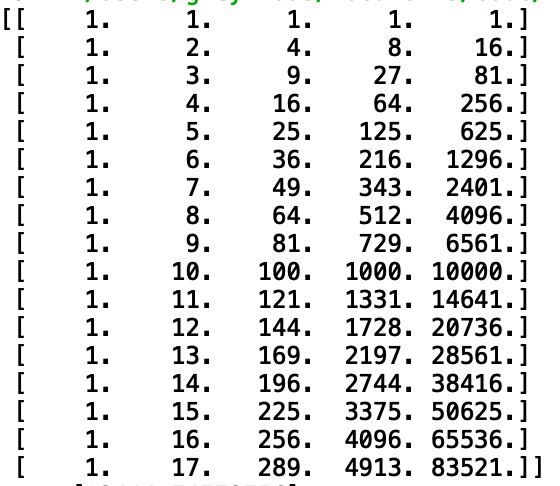
  回归分析

  接下来把x_poly作为一个多元变量，进行线性回归即可
  首先是模型的训练

  clf = LinearRegression()
  clf.fit(x_poly,data[rown].reshape(-1,1))
  

  训练完成后可以预测结果

  day_range=np.linspace(begin_day,begin_day + day_num - 1,day_num)
  result = clf.predict(poly_reg.fit_transform(day_range.reshape(-1,1)))
  

  获取线性回归模型的具体参数

  clf.coef_ #参数
  clf.intercept_ #截距
  

  画图

  plt.plot(np.arange(1,len(data[0])+1),data[rown],color='g',linestyle='--',marker='o',label='true')
  plt.plot(day_range,result,color=color,linestyle='--',marker='.',label='predict')
  plt.title("2019-nCov")
  plt.legend()
  plt.show()
  

  训练数据

  数据来源于卫健委每日发布的数据，记录成csv格式
  第一行相当于自变量x，对应着第i天
  第二行为武汉市的确诊人数，第三行是全国的确诊人数，第四行是疑似病例

  1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21
  27,41,45,62,121,198,258,363,425,495,572,618,698,1590,1905,2261,2639,3215,4109,5142,6384
  27,41,45,62,121,198,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791,14380,17205,20438
  0,0,0,0,0,0,54,37,393,1072,1965,2684,5794,6973,9239,12167,15238,17988,19544,21588,23214
  

  预测结果

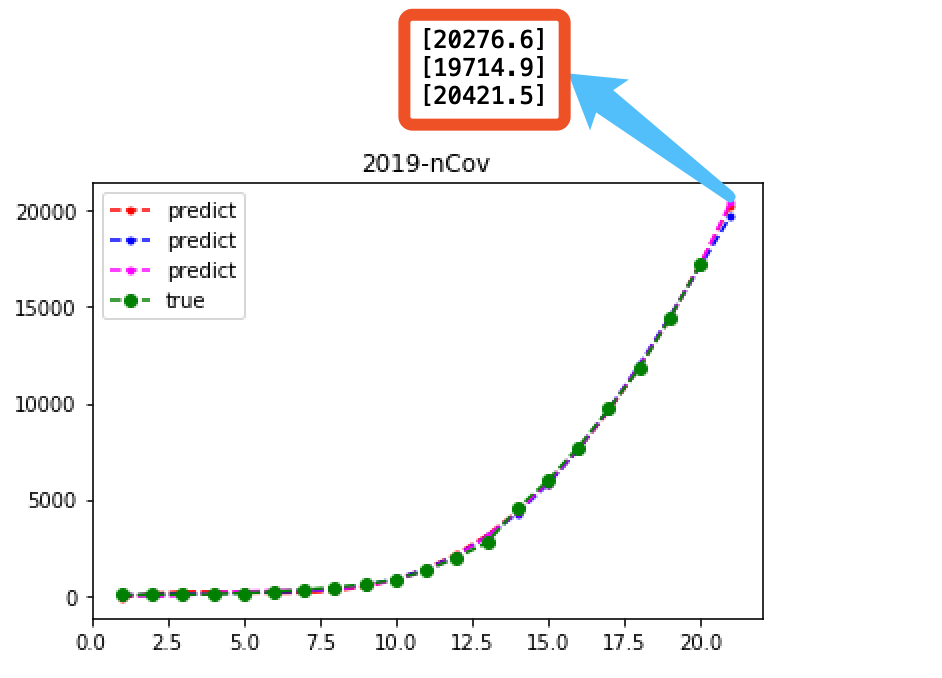  实际人数：20438人

  /	2020/1/29	2020/1/30	2020/1/31	2020/2/1	2020/2/2	2020/2/3
  4次回归	8448.4	10365.7	12444.7	14578.9	17254.8	20276.6
  5次回归	8305.4	9769.4	11623	13631.5	16491.4	19714.9
  6次回归	7658.5	8922.6	11065.7	13412.3	16865.1	20421.5
  7次回归	6790	8537.5	11540.7	14280.6	18131.7	21436.5
  真实	7711	9692	11791	14380	17205	20438

  原始代码

  import numpy as np
  from sklearn.preprocessing import PolynomialFeatures
  from sklearn.linear_model import LinearRegression
  from matplotlib import pyplot as plt
  
  def predict_new(clf,data,rown,degree,color):
      begin_day = 1
      day_num = 22
      poly_reg = PolynomialFeatures(degree=degree)
      x_poly = poly_reg.fit_transform(data[0].reshape(-1,1))
      #print(x_poly)
      clf.fit(x_poly,data[rown].reshape(-1,1))
      day_range=np.linspace(begin_day,begin_day + day_num - 1,day_num) # [1,2,...,day_num]
      result = clf.predict(poly_reg.fit_transform(day_range.reshape(-1,1)))
      print("                            ",np.around(result[-1],decimals=1))
      plt.plot(day_range,result,color=color,linestyle='--',marker='.',label='predict')
      
  def predict(clf,data):
      rown=2
      plt.figure()
      predict_new(clf,data,rown,4,'red')
      predict_new(clf,data,rown,5,'blue')
      predict_new(clf,data,rown,6,'fuchsia')
      predict_new(clf,data,rown,7,'orange')
      plt.plot(np.arange(1,len(data[0])+1),data[rown],color='g',linestyle='--',marker='o',label='true') # 画出真实值
      plt.title("2019-nCov")
      plt.legend()
      plt.show()
      
  def read_data():
      with open("data.csv","r") as f:
          data = np.loadtxt(f,delimiter = ",")
          data = data[...,:] # 对数据切片，回溯前几天的预测值，对比准确性时用到
          print()
          return data
          
  if __name__ == "__main__":
      print()
      np.set_printoptions(suppress=True)
      data =read_data()
      clf = LinearRegression()
      predict(clf,data)
  
  

  参考

  Sklearn实现非线性回归

  Read All

  ---

• 【Python】csv文件的读写

  2020-01-28

  技巧

  Python
  • 使用传统csv模块
  • 使用numpy
    • 例子
    • converters函数
    • numpy切片
    • pandas

  使用传统csv模块

  其中newline在linux/mac系统下可不加，用于去除windows系统下的多余换行

  import csv
  with open(csvname,"a+",newline="") as file:
      writer = csv.writer(file)
      writer.writerow(content)
  

  使用numpy

  import numpy as np
  with open("1.csv","r") as f:
      res = np.loadtxt(f,delimiter = ",")
  

  • delimiter 分隔符，默认是空格
  • skiprows 跳过前N行，默认为0
  • comments 设置评论行，如果值为’#’,则#开头的行不读取
  • usecols 只使用其中几列，值为一个tuple,如(0,2)
  • unpack 如果为True，则不返回二维矩阵，把每一列当成一个向量输出，使用一个tuple来接受返回值
  • dtype 类型

  例子

  例如某csv文件

  #AA BB CC
  A B C
  1 2 3 
  4 5 6
  7 8 9 
  

  读取代码

  (a,b) = np.loadtxt('1.csv',delimiter=' ',comments='#,usecols=(0,2),unpack=True)
  print(a,b)
  

  输出

  [1 4 7] [3 6 9]
  

  converters函数

  对指定列的数据进行预处理的参数

  def do_something(x):
      pass
  # 对第0列的数据进行处理
  converters={0:do_someting}
  

  numpy切片

  主要是对二维数组按列进行切片，使用省略号来进行切片。

  a = np.array([[1,2,3],[3,4,5],[4,5,6]])  
  print (a[...,1])   # 第2列元素
  print (a[1,...])   # 第2行元素
  print (a[...,1:])  # 第2列及剩下的所有元素
  

  一维的切片方式为：

  a = np.arange(10)  
  # 从索引 2 开始到索引 7 停止，间隔为 2
  b = a[2:7:2]   
  print(b)
  # 输出：2 4 6
  

  pandas

  import pandas as pd
  
  df = pd.read_csv(filename,usecols=[要取的列名])
  df = pd.read_csv('1.csv',usecols=['teacher','student'])
  

  参数：

  • header 指定行数作为列名，如果文件中没有列名，则默认为0
  Read All

  ---

• 【深度学习】使用Yolo v5进行目标检测

  2020-01-19

  技巧

  机器学习

  使用使用Yolo v5进行目标检测

  环境

  为了快速使用YOLO的环境，使用docker进行部署

  拉取镜像

  docker pull ultralytics/yolov5:latest
  

  镜像比较大，有14.5GB，所以需要更改镜像源为阿里云的镜像（测试时只有这个比较快）

  快速运行

  启动docker，并将当前目录挂载到/usr/src/coco目录下

  docker run --ipc=host -it -v "$(pwd)":/usr/src/coco ultralytics/yolov5:latest
  

  然后利用预训练的模型对图像进行检测

  python detect.py --source [文件名]
  

  第一次运行会自动从github下载v5s模型，国内下载的速度比较慢，可以通过其他途径下好后放入/usr/src/app目录下

  docker cp yolov5s.pt [容器名]:/usr/src/app
  

  下载地址

  • yolo v5s
  • yolo v5m
  • yolo v5l
  • yolo v5x

  结果放在/usr/src/app/runs/detect/exp目录中

  Read All

  ---

• 【Python】numpy笔记

  2020-01-04

  笔记

  Python
  • 属性查询
  • 生成
  • 矩阵增删改查
    • 增
    • 加法
    • 查
    • 改
    • 删
    • 多维数组降为1维
  • 矩阵转置
  • 矩阵乘法
  • 求矩阵的特征值和特征向量
  • matrix 转换为数组
  • 精度控制
  • 关闭科学技术法

  随用随记

  import numpy as np
  

  属性查询

  a1 = np.array([1,2,3,4],dtype=np.complex128)  
  print(a1)  
  print("数据类型",type(a1))           #打印数组数据类型  
  print("数组元素数据类型：",a1.dtype) #打印数组元素数据类型  
  print("数组元素总数：",a1.size)      #打印数组尺寸，即数组元素总数  
  print("数组形状：",a1.shape)         #打印数组形状  
  print("数组的维度数目",a1.ndim)      #打印数组的维度数目 
  print("数组的行数",np.shape(a1)[0]) #打印数组的行数 
  print("数组的列数",np.shape(a1)[1]) #打印数组的列数
  

  生成

  a = np.zeros(6)#创建长度为6的，元素都是0一维数组
  a = np.zeros((2,3))#创建2行3列，元素都是0的二维数组
  a = np.ones((2,3))#创建2行3列，元素都是1的二维数组
  a = np.empty((2,3)) #创建2行3列,未初始化的二维数组
  a = np.arange(6)#创建长度为6的，元素都是0一维数组array([0, 1, 2, 3, 4, 5])
  a = np.arange(1,7,1)#结果与np.arange(6)一样。第一，二个参数意思是数值从1〜6,不包括7.第三个参数表步长为1.
  a = np.linspace(0,10,7) # 生成首位是0，末位是10，含7个数的等差数列[  0.           1.66666667   3.33333333   5.         6.66666667  8.33333333  10.        ]
  a = np.logspace(0,4,5) # 用于生成首位是10**0，末位是10**4，含5个数的等比数列。
  a = np.random.randint(1, 100, (3, 3)) # 生成形状为3x3的二维整数数组
  

  矩阵增删改查

  增

  >>> a = np.array([[1,2],[3,4],[5,6]])
  >>> b = np.array([[10,20],[30,40],[50,60]])
  >>> np.vstack((a,b))
  array([[ 1,  2],
         [ 3,  4],
         [ 5,  6],
         [10, 20],
         [30, 40],
         [50, 60]])
  >>> np.hstack((a,b))
  array([[ 1,  2, 10, 20],
         [ 3,  4, 30, 40],
         [ 5,  6, 50, 60]])
  

  加法

  >>> a = np.array([[1],[2]])
  >>> a
  array([[1],
         [2]])
  >>> b=([[10,20,30]])#生成一个list，注意，不是np.array。
  >>> b
  [[10, 20, 30]]
  >>> a+b
  array([[11, 21, 31],
         [12, 22, 32]])
  >>> c = np.array([10,20,30])
  >>> c
  array([10, 20, 30])
  >>> c.shape
  (3,)
  >>> a+c
  array([[11, 21, 31],
         [12, 22, 32]])
  

  查

  
  >>> a
  array([[1, 2],
         [3, 4],
         [5, 6]])
  >>> a[0] # array([1, 2])
  >>> a[0][1]#2
  >>> a[0,1]#2
  >>> b = np.arange(6)#array([0, 1, 2, 3, 4, 5])
  >>> b[1:3]#右边开区间array([1, 2])
  >>> b[:3]#左边默认为 0array([0, 1, 2])
  >>> b[3:]#右边默认为元素个数array([3, 4, 5])
  >>> b[0:4:2]#下标递增2array([0, 2])
  

  改

  >>> a = np.array([[1,2],[3,4],[5,6]])
  >>> a[0] = [11,22]#修改第一行数组[1,2]为[11,22]。
  >>> a[0][0] = 111#修改第一个元素为111,修改后，第一个元素“1”改为“111”。
   
  >>> a = np.array([[1,2],[3,4],[5,6]])
  >>> b = np.array([[10,20],[30,40],[50,60]])
  >>> a+b #加法必须在两个相同大小的数组键间运算。
  array([[11, 22],
         [33, 44],
         [55, 66]])
  

  删

  >>> a = np.array([[1,2],[3,4],[5,6]])
  >>> np.delete(a,1,axis = 0)#删除a的第二行。
  array([[1, 2],
         [5, 6]])
  >>> np.delete(a,(1,2),0)#删除a的第二，三行。
  array([[1, 2]])
  >>> np.delete(a,1,axis = 1)#删除a的第二列。
  array([[1],
         [3],
         [5]])
  

  多维数组降为1维

  .ravel()和.flatten()

  a = np.array([[1,2,3],[11,22,33]])
  print(a.ravel())
  print(a.flatten())
  

  输出都是

  [ 1 2 3 11 22 33]
  

  不同点ravel会修改原数组，而flatten不会

  矩阵转置

  a.T
  

  矩阵乘法

  a = np.mat([1,2,3])
  b = np.mat([4,5,6])
  ret = np.dot(a,b)
  

  求矩阵的特征值和特征向量

  a为特征值
  b为特征向量

  a,b = np.linalg.eig(ret)
  

  matrix 转换为数组

  arr = ret.getA()
  

  精度控制

  对ret保留小数点后两位

  np.around(ret,decimals = 2)
  

  关闭科学技术法

  np.set_printoptions(suppress=True)
  

  Read All

  ---

• 论文记录

  2019-12-25

  学术

  粗读
  • 综述
    • 深度包检测中正则表达式匹配的算法、应用和硬件平台的综述
    • 基于模型的定量网络安全度量研究综述
    • 自适应比特率选择的综述
    • 利用机器学习技术进行入侵检测的详细调查与分析

  此页用于记录一些看到的比较好的论文,作为自己的论文库

  综述

  深度包检测中正则表达式匹配的算法、应用和硬件平台的综述

  2016 S&T
  原文地址：A Survey on Regular Expression Matching for Deep Packet Inspection: Applications, Algorithms, and Hardware Platforms

  摘要：

  本次调查从DPI的全面应用背景和正则表达式匹配的技术背景入手，为读者提供一个全局视图和基本知识。然后分析了有限状态自动机用于正则表达式匹配的状态爆炸对正则表达式匹配的挑战。详细分析了状态爆炸的本质，将最新的解决方案分为缓解状态爆炸的方法和避免状态爆炸的方法两大类，并提出了在不同场景下构建紧凑高效自动机的建议。此外，还介绍并深入讨论了采用并行平台（包括现场可编程门阵列、GPU、通用多处理器和三值内容寻址存储器）加速匹配过程的建议。我们还为每个平台的高效部署提供了指导。

  基于模型的定量网络安全度量研究综述

  2017 S&T 原文地址：Model-Based Quantitative Network Security Metrics: A Survey

  摘要：

  基于模型的网络安全度量（NSMs）可以定量评估网络系统抵御攻击的总体弹性。因此，这些度量对于组织的安全相关决策过程非常重要。考虑到近20年来已经提出了一些基于模型的定量NSMs，本文对这些方案的研究现状进行了深入的综述。首先，为了将本调查中描述的安全度量与其他类型的安全度量区分开来，本文概述了安全度量及其分类。然后，详细介绍了现有的基于模型的定量NSMS，以及它们的优缺点。最后，对本次调查的相关特点进行了深入的探讨，提出了本次调查的建议和课题的开放性研究问题。

  自适应比特率选择的综述

  2017 S&T 原文地址：Adaptive Bitrate Selection: A Survey

  摘要：

  HTTP自适应流（HAS）是最新的视频质量自适应尝试。它支持廉价且易于实现的流媒体技术，而无需专用的基础设施。通过TCP和HTTP的组合，它具有所有为普通Web设计的现有技术的优点。同样重要的是，流量可以通过防火墙，并且在部署NAT时工作良好。HAS的速率自适应控制器，通常称为自适应比特率选择（ABR），目前正受到业界和学术界的广泛关注。然而，大多数研究工作都集中在某一特定方面或某一特定方法上，而没有考虑到整个背景。本文综述了基于客户端HTTP的自适应视频流领域最重要的研究活动。它首先将ABR模块分解为三个子组件，即：资源估计功能、块请求调度和自适应模块。每个子组件封装对ABR方案的操作至关重要的特定函数。对每一个子组件以及它们如何相互作用进行了回顾。此外，还讨论了已知对ABR模块的性能有直接影响的外部因素，例如内容性质、CDN和上下文。总之，本文为该领域的进一步研究提供了广泛的参考。

  利用机器学习技术进行入侵检测的详细调查与分析

  2018 S&T 原文地址: A Detailed Investigation and Analysis of Using Machine Learning Techniques for Intrusion Detection

  Read All

  ---